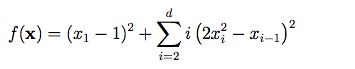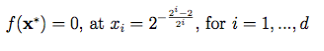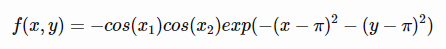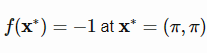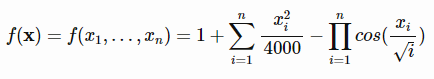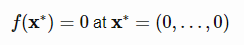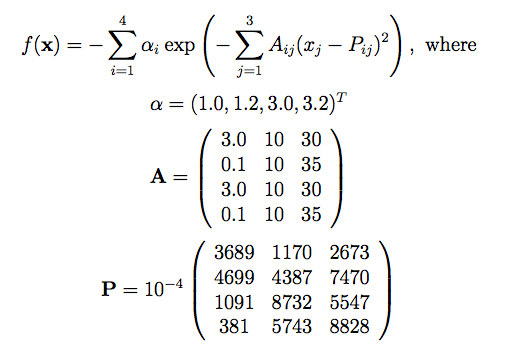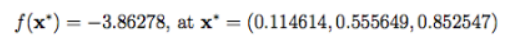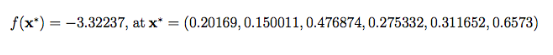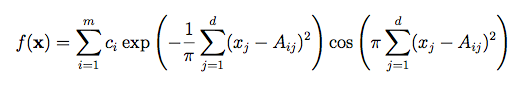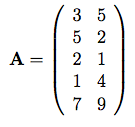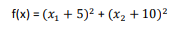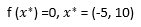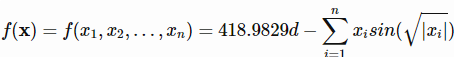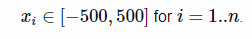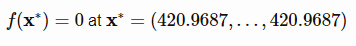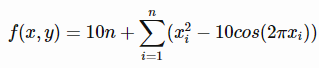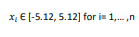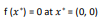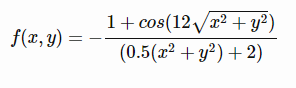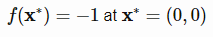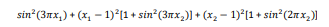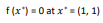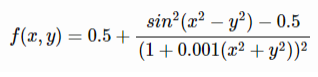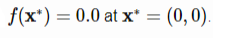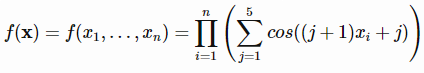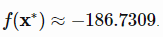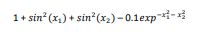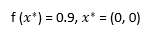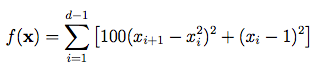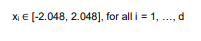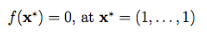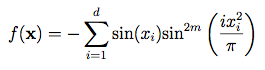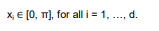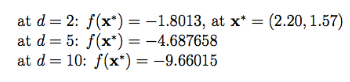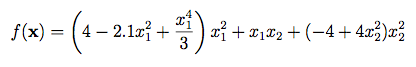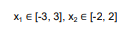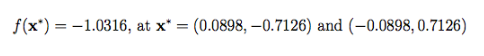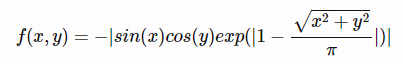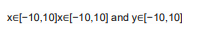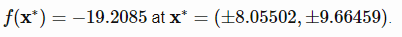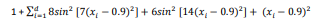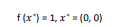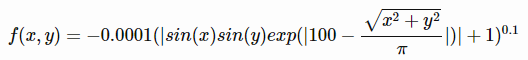VQ: Vector Quantization

چندی سازی برداری

VQ: Vector Quantization

چندی سازی برداری

معرفی توابع بنچمارک

توابع بنچ مارک یک سری توابع ریاضی می باشند که از آنها برای تست پروسیجرهای بهینه سازی استفاده می گردد که در ادامه تعدادی از این توابع را معرفی می کنیم

 

تابع Shekel’s foxholes

 تابع تست چند حالته می باشد  که به صورت زیر می باشد

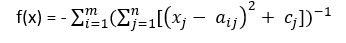
مقادیر ثابت از پیش تعیین شده می باشند. توصیه می شود که مقدار m=30 باشد

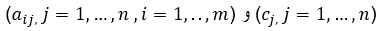
  تابع Goldstein-Price

   این تابع برای تست بهینه سراسری استفاده می گردد. این تابع فقط دارای دو متغییر می باشد که به صورت زیر می باشد 

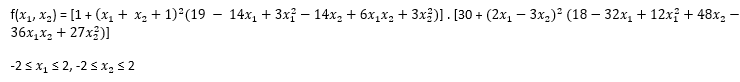
مینیمم سراسری آن برابر با f(x)=3 در نقطه (1,0) = (x1 , x2)می باشد

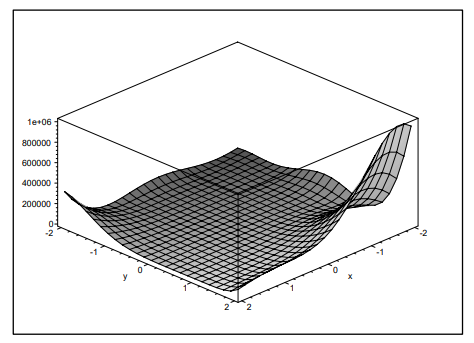
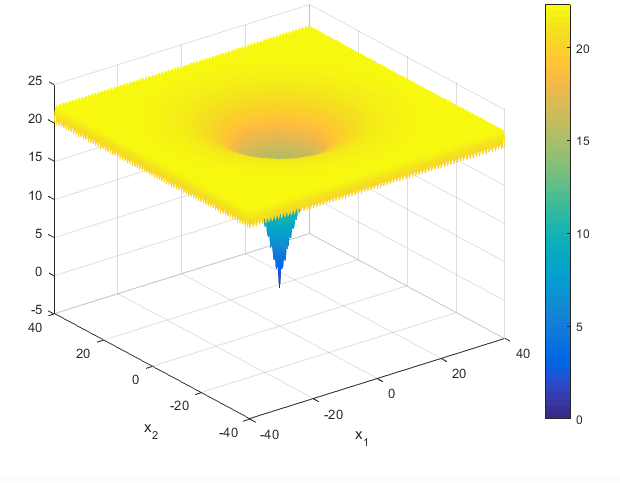
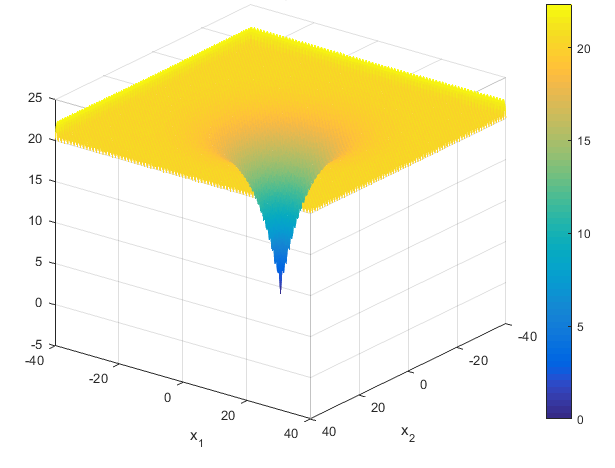
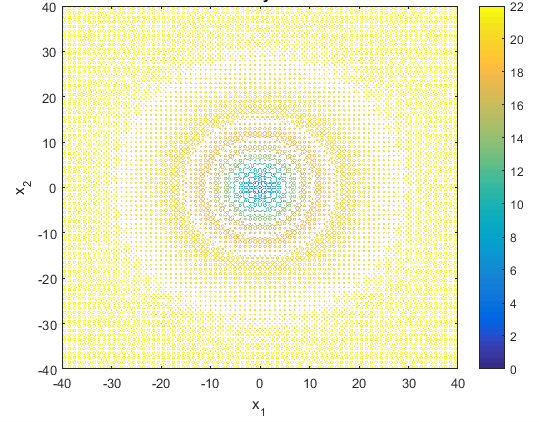
 تابع Ackley

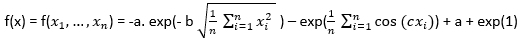
مقادیر a، b و c ثابت بوده و به صورت زیر می باشند

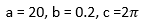
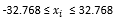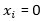معمولاi=1,...,n ,  می باشد. مینیمم سراسری برای آن f(x) = 0 برای i= 0,..,n ،    بدست می آید

کد آن در محیط متلب به صورت زیر می باشد

function scores = ackleyfcn(x)

    n = size(x, 2);

    ninverse = 1 / n;

    sum1 = sum(x .^ 2, 2);

    sum2 = sum(cos(2 * pi * x), 2);

   

    scores = 20 + exp(1) - (20 * exp(-0.2 * sqrt( ninverse * sum1))) - exp( ninverse * sum2);

end


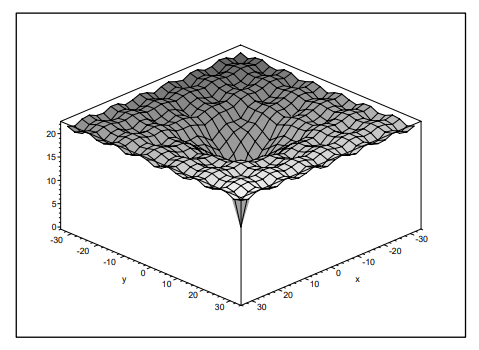
  تابع Beale

 فورمول این تابع به صورت زیر می باشد

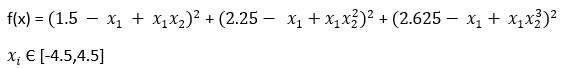
            دوبعدی می باشد. عملکرد Beale چند حالته است و قله های تیز در گوشه و کنار دامنه ورودی وجود دارد.

            مقدار مینیمم سراسری آن به صورت زیر می باشد

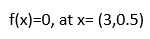
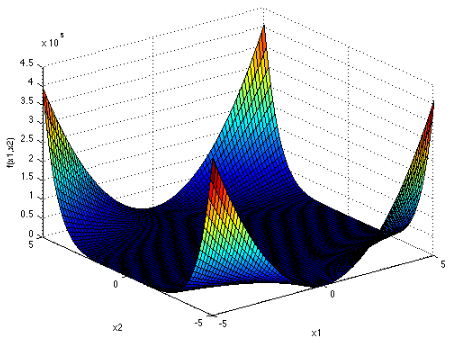
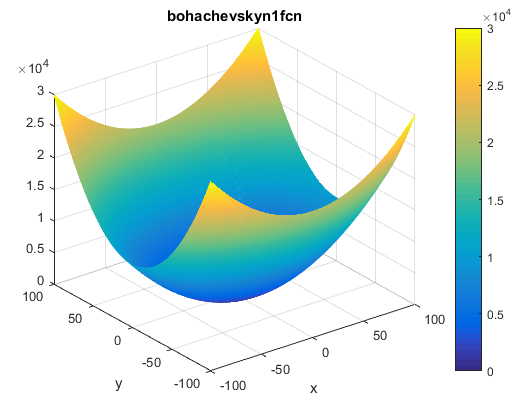
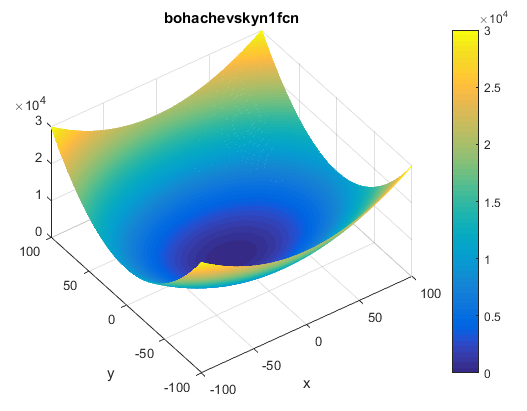
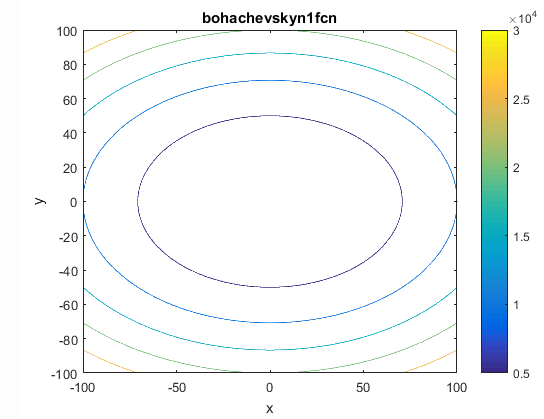
  تابع Bohachevsky N. 1

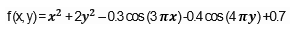
                  این تابع پیوسته و محدب می باشد و در فضای دوبعدی تعریف شده است. این تابع غیربدیل می باشد.

                 دامنه ورودی

                     این تابع می تواند روی هر ورودی تعریف شود ولی معمولا به صورت زیر تعریف می گردد.

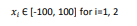
                 مینیمم سراسری

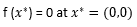
                کد آن در متلب به صورت زیر می باشد

% Computes the value of Bohachevsky N. 1 benchmark function.
% SCORES = BOHACHEVSKYN1FCN(X) computes the value of the Bohachevsky N. 1
% function at point X. BOHACHEVSKYN1FCN accepts a matrix of size M-by-N and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for each row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = bohachevskyn1fcn(x)
    n = size(x, 2);
    assert(n == 2, 'The Bohachevsky N. 1 function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    scores = (X .^ 2) + (2 * Y .^ 2) - (0.3 * cos(3 * pi * X)) - (0.4 * cos(4 * pi * Y)) + 0.7;
end

 


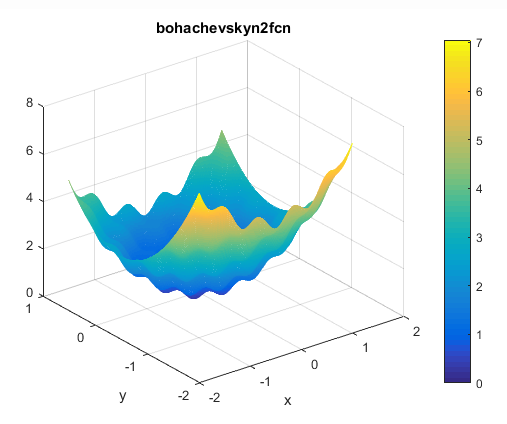
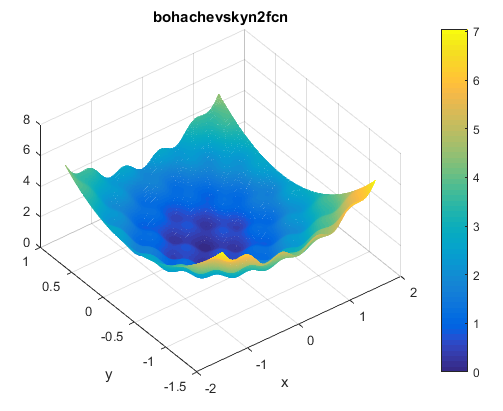
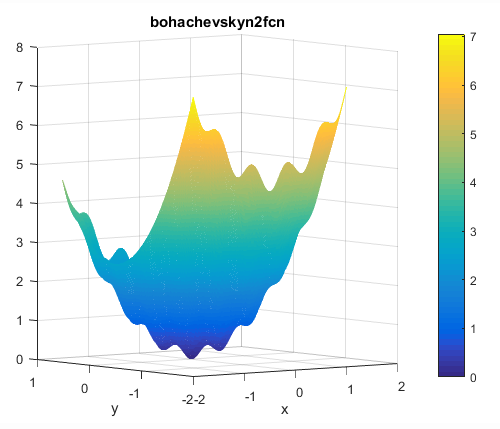
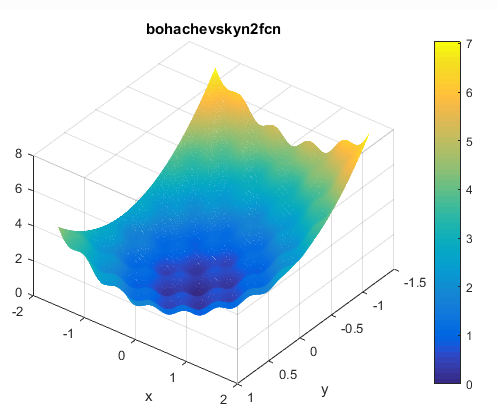
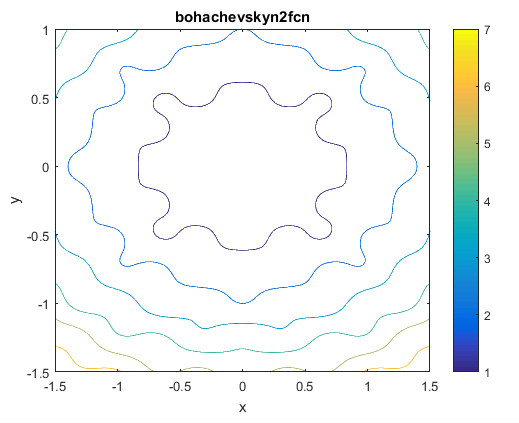
Bohachevsky N.2

                این تابع به صورت زیر تعریف می شود

 

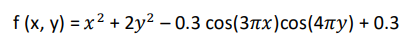
                       ویژگی های آن

                                         1.این تابع به صورت محدب می باشد.

                                         2.این تابع در فضای دوبعدی تعریف شده است.

                                          3.این تابع غیر قابل تفکیک می باشد

                                          4.این تابع تشخیص پذیر(differentiable) می باشد

            دامنه ورودی

                 این تابع می تواند روی هر ورودی تعریف شود ولی معمولا به صورت زیر تعریف می گردد

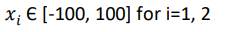
          مینیمم سراسری

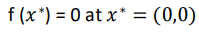
         کد آن در متلب به صورت زیر می باشد

% Computes the value of Bohachevsky N. 2 benchmark function.
% SCORES = BOHACHEVSKYN2FCN(X) computes the value of the Bohachevsky N. 2
% function at point X. BOHACHEVSKYN2FCN accepts a matrix of size M-by-N and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for each row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = bohachevskyn2fcn(x)
    n = size(x, 2);
    assert(n == 2, 'The Bohachevsky N. 2 function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    scores = (X .^ 2) + (2 * Y .^ 2) - (0.3 * cos(3 * pi * X)) .* (cos(4 * pi * Y)) + 0.3;
end

  

تابع Bohachevsky N.3

           این تابع به صورت زیر می باشد

           ویژگی های آن

1.این تابع به صورت محدب می باشد.

2.این تابع در فضای دوبعدی تعریف شده است.

           دامنه ورودی

              این تابع می تواند روی هر ورودی تعریف شود ولی معمولا به صورت زیر تعریف می گردد

    

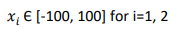
           مینیمم سراسری

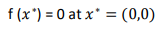
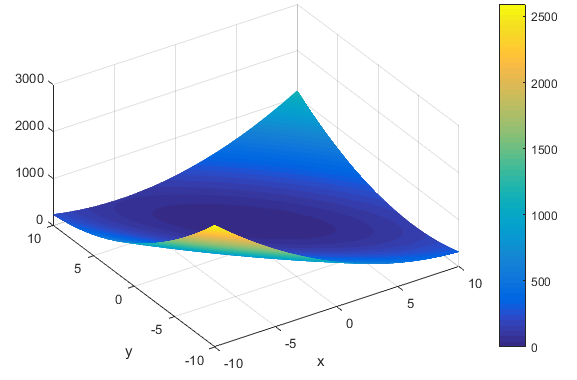
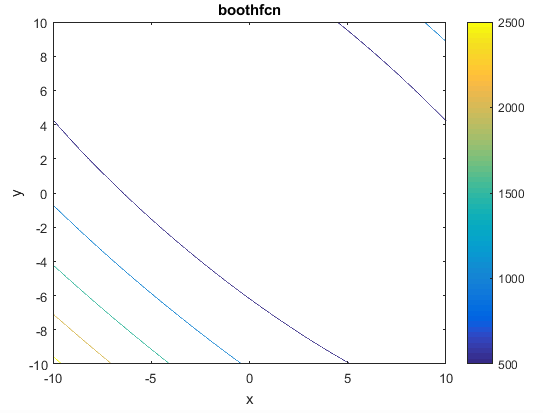
    تابع Booth

              این تابع به صورت زیر می باشد

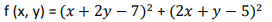
 ویژگی های آن

1.                                                          این تابع پیوسته می باشد

2.                                                          این تابع به صورت محدب می باشد.

3.                                                         این تابع در فضای دوبعدی تعریف شده است.

4.                                                          این تابع غیربدیل می باشد

5.                                                         این تابع تشخیص پذیر(differentiable) می باشد

 دامنه ورودی

      این تابع می تواند روی هر ورودی تعریف شود ولی معمولا به صورت زیر تعریف می گردد

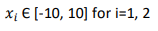
مینیمم سراسری

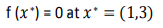
کد آن در متلب به صورت زیر می باشد

% Computes the value of the Booth benchmark function.
% SCORES = BOOTHFCN(X) computes the value of the Booth's function at 
% point X. BOOTHFCN accepts a matrix of size M-by-2 and returns a  
% vetor SCORES of size M-by-1 in which each row contains the function value 
% for the corresponding row of X.
% For more information please visit: 
% https://en.wikipedia.org/wiki/Test_functions_for_optimization
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = boothfcn(x)
    
    n = size(x, 2);
    assert(n == 2, 'Booth''s function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    scores = (X + (2 * Y) - 7).^2 + ( (2 * X) + Y - 5).^2;
end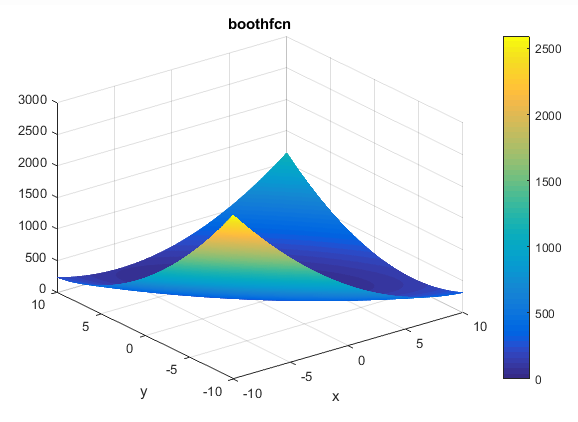


 تابع Branin

تابع به صورت زیر می باشد


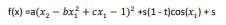
این تابع دارای سه مینیمم سراسری می باشد. مقادیر a، b، c، r،  s، t توصیه می شود مقادیر زیر باشند

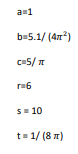
             دامنه ورودی

                    معمولا مربع زیر می باشد

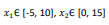
مینیمم سراسری

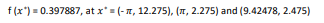
کد متلب آن به صورت زیر می باشد

function [y] = branin(xx, a, b, c, r, s, t)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% BRANIN FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUTS:
%
% xx = [x1, x2]
% a = constant (optional), with default value 1
% b = constant (optional), with default value 5.1/(4*pi^2)
% c = constant (optional), with default value 5/pi
% r = constant (optional), with default value 6
% s = constant (optional), with default value 10
% t = constant (optional), with default value 1/(8*pi)
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x1 = xx(1);
x2 = xx(2);
 
if (nargin < 7)
    t = 1 / (8*pi);
end
if (nargin < 6)
    s = 10;
end
if (nargin < 5)
    r = 6;
end
if (nargin < 4)
    c = 5/pi;
end
if (nargin < 3)
    b = 5.1 / (4*pi^2);
end
if (nargin < 2)
    a = 1;
end
 
term1 = a * (x2 - b*x1^2 + c*x1 - r)^2;
term2 = s*(1-t)*cos(x1);
 
y = term1 + term2 + s;
 
end

 

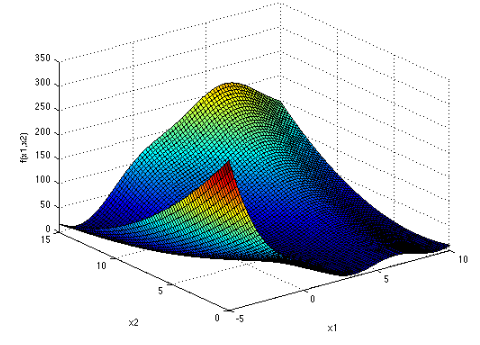
تابع Colville

این تابع به صورت زیر می باشد

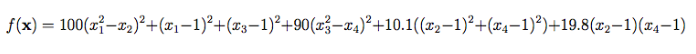
ابعاد: 4

مینیمم سراسری

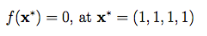
کد متلب آن به صورت زیر می باشد

function [y] = colville(xx)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% COLVILLE FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUTS:
%
% xx = [x1, x2, x3, x4]
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x1 = xx(1);
x2 = xx(2);
x3 = xx(3);
x4 = xx(4);
 
term1 = 100 * (x1^2-x2)^2;
term2 = (x1-1)^2;
term3 = (x3-1)^2;
term4 = 90 * (x3^2-x4)^2;
term5 = 10.1 * ((x2-1)^2 + (x4-1)^2);
term6 = 19.8*(x2-1)*(x4-1);
 
y = term1 + term2 + term3 + term4 + term5 + term6;
 

end
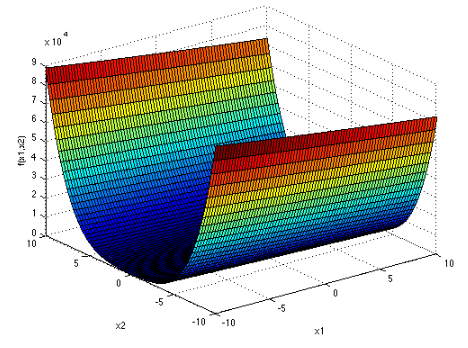
  تابع Dixon-Price
تابع آن به صورت زیر می باشد



       ابعاد :d
       دامنه ورودی:
    
مینیمم سراسری            



کد متلب آن به صورت زیر می باشد


function [y] = dixonpr(xx)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% DIXON-PRICE FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUT:
%
% xx = [x1, x2, ..., xd]
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x1 = xx(1);
d = length(xx);
term1 = (x1-1)^2;
 
sum = 0;
for ii = 2:d
        xi = xx(ii);
        xold = xx(ii-1);
        new = ii * (2*xi^2 - xold)^2;
        sum = sum + new;
end
 
y = term1 + sum;
 
end


  تابع Easom
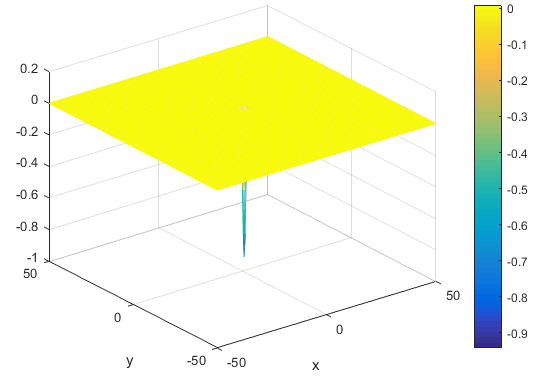
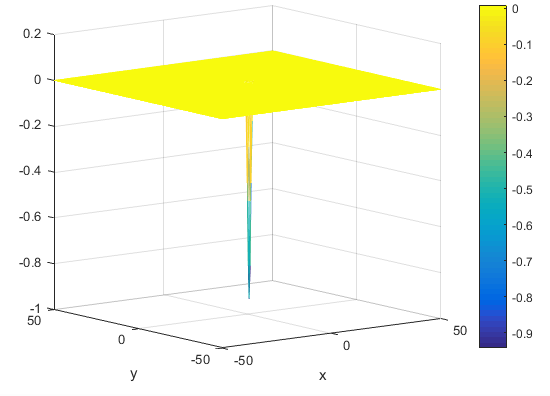
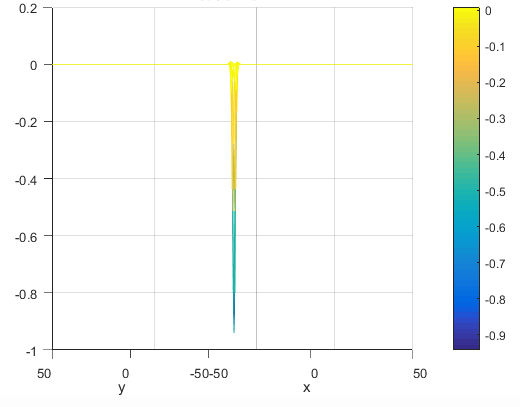
اینتابع به صورت زیر می باشد
ویژگی های آن

این تابع پیوسته می باشد
این تابع به صورت محدب میباشد. 
این تابع در فضای دوبعدیتعریف شده است. 
این تابع جند حالته می باشد
این تابع تشخیص پذیر(differentiable) می باشد
این تابع تفکیک ناپذیراست
             این تابع مقیاس ناپذیراست
     دامنه ورودی
 این تابع می تواند روی هر ورودی تعریف شود ولی معمولا به صورت زیر تعریف می گردد
     مینیمم سراسری
  کد آن در متلب به صورت زیر می باشد



% Computes the value of the Easom benchmark function.



% SCORES = EASOMFCN(X) computes the value of the Easom
function at point X.



% EASOMFCN accepts a matrix of size M-by-2 and returns a
vetor SCORES of 



% size M-by-1 in which each row contains the function value
for the 



% corresponding row of X. For more information please
visit: 



%
https://en.wikipedia.org/wiki/Test_functions_for_optimization



% 



% Author: Mazhar Ansari Ardeh



% Please forward any comments or bug reports to
mazhar.ansari.ardeh at



% Google's e-mail service or feel free to kindly modify the
repository.



function scores = easomfcn(x)



    



    n = size(x, 2);



    assert(n == 2, 'The Easom''s function is only defined on a 2D
space.')



    X = x(:, 1);



    Y = x(:, 2);



    



    scores = -cos(X) .* cos(Y) .*
exp(-( ((X - pi) .^2) +
((Y - pi) .^ 2)) );



end


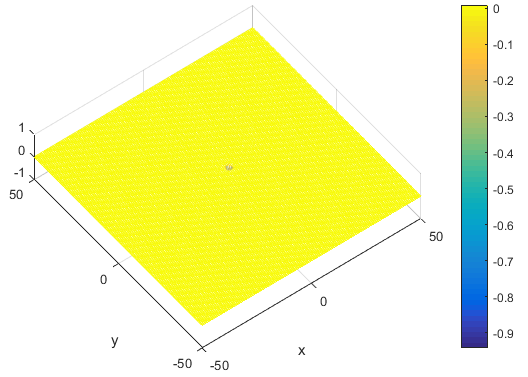
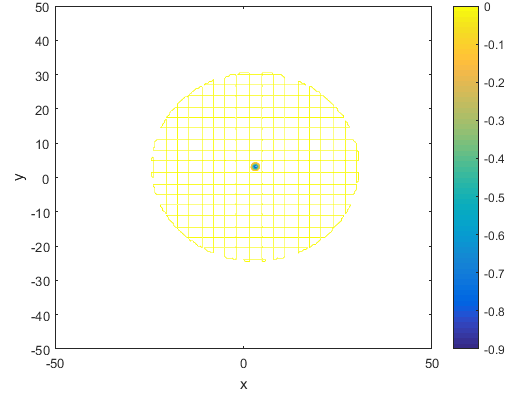
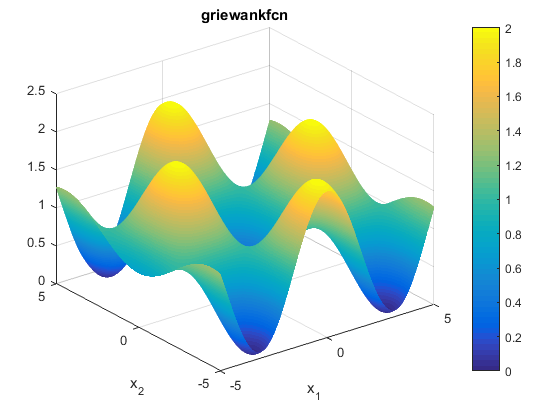
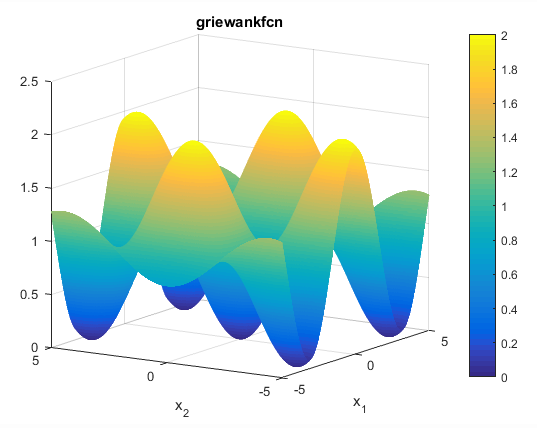
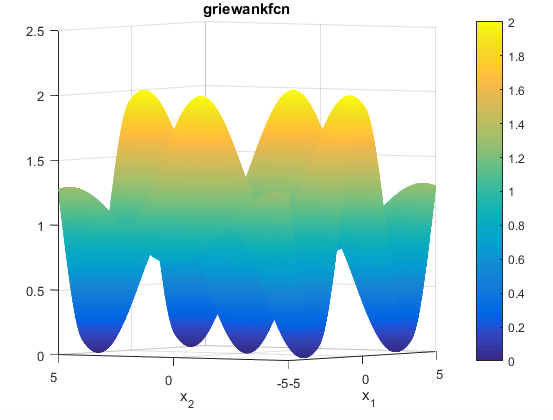
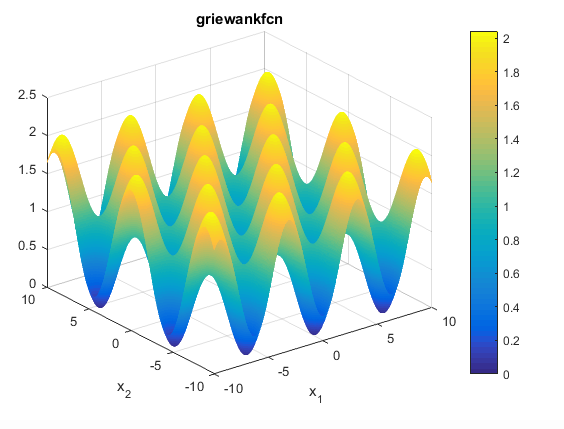
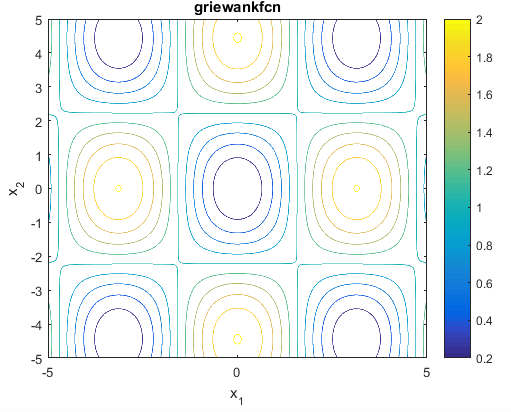
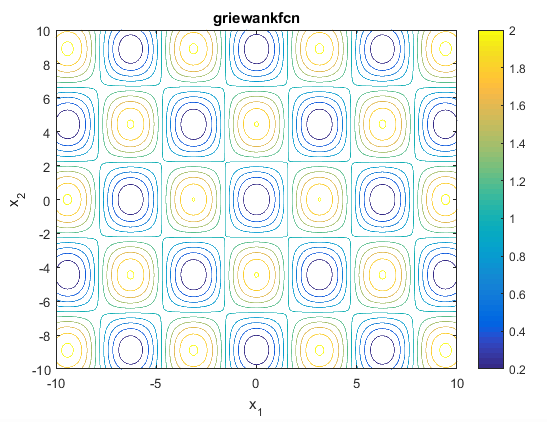
تابع Griewank
این تابع به صورت زیر می باشد


ویژگی های آن 
  1. این تابع پیوسته می باشد
  2.این تابع به صورت محدب می باشد. 
  3.این تابع در فضای nبعدی تعریف شده است. 
  4.این تابع غیربدیل(unimodal) می باشد
            دامنه ورودی
     این تابع می تواند روی هر ورودی تعریف شود ولی معمولا به صورت زیر تعریف می گردد
مینیمم سراسری

کد متلب آن به صورت زیر می باشد

% Computes the value of the Griewank benchmark function.
% SCORES = GRIEWANKFCN(X) computes the value of the Griewank's
% function at point X. GRIEWANKFCN accepts a matrix of size M-by-N 
% and returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = griewankfcn(x)
    
    n = size(x, 2);
    
    sumcomp = 0;
    prodcomp = 1;
    
    for i = 1:n
        sumcomp = sumcomp + (x(:, i) .^ 2);
        prodcomp = prodcomp .* (cos(x(:, i) / sqrt(i)));
    end
    
    scores = (sumcomp / 4000) - prodcomp + 1;
end

تابع Hartman3
 تابع آن به صورت زیر می باشد





ویژگی ها 
  1.ابعاد 3
  2.دارای 4 مینیمم محلی می باشد
دامنه ورودی
مینیمم سراسری
کد متلب آن به صورت زیر می باشد
function [y] = hart3(xx)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% HARTMANN 3-DIMENSIONAL FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUT:
%
% xx = [x1, x2, x3]
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
alpha = [1.0, 1.2, 3.0, 3.2]';
A = [3.0, 10, 30;
     0.1, 10, 35;
     3.0, 10, 30;
     0.1, 10, 35];
P = 10^(-4) * [3689, 1170, 2673;
               4699, 4387, 7470;
               1091, 8732, 5547;
               381, 5743, 8828];
 
outer = 0;
for ii = 1:4
        inner = 0;
        for jj = 1:3
               xj = xx(jj);
               Aij = A(ii, jj);
                Pij = P(ii, jj);
               inner = inner + Aij*(xj-Pij)^2;
        end
        new = alpha(ii) * exp(-inner);
        outer = outer + new;
end
 
y = -outer;
 
end
تابع Hartman6
تابع آن به صورت زیر می باشد
ویژگی ها
   1.ابعاد: 6
   2.دارای 6 مینیمم محلی میباشد
      دامنه ورودی
      مینیمم سراسری
ویرایش شده آن

کد متلب آن به صورت زیر میباشد

function [y] = hart6(xx)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% HARTMANN 6-DIMENSIONAL FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUT:
%
% xx = [x1, x2, x3, x4, x5, x6]
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
alpha = [1.0, 1.2, 3.0, 3.2]';
A = [10, 3, 17, 3.5, 1.7, 8;
     0.05, 10, 17, 0.1, 8, 14;
     3, 3.5, 1.7, 10, 17, 8;
     17, 8, 0.05, 10, 0.1, 14];
P = 10^(-4) * [1312, 1696, 5569, 124, 8283, 5886;
               2329, 4135, 8307, 3736, 1004, 9991;
               2348, 1451, 3522, 2883, 3047, 6650;
               4047, 8828, 8732, 5743, 1091, 381];
 
outer = 0;
for ii = 1:4
        inner = 0;
        for jj = 1:6
               xj = xx(jj);
               Aij = A(ii, jj);
               Pij = P(ii, jj);
               inner = inner + Aij*(xj-Pij)^2;
        end
        new = alpha(ii) * exp(-inner);
        outer = outer + new;
end
 
y = -(2.58 + outer) / 1.94;
 
end
کد متلب ویراش شده آن
function [y] = hart6sc(xx)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% HARTMANN 6-DIMENSIONAL FUNCTION, RESCALED
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUT:
%
% xx = [x1, x2, x3, x4, x5, x6]
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
alpha = [1.0, 1.2, 3.0, 3.2]';
A = [10, 3, 17, 3.50, 1.7, 8;
     0.05, 10, 17, 0.1, 8, 14;
     3, 3.5, 1.7, 10, 17, 8;
     17, 8, 0.05, 10, 0.1, 14];
P = 10^(-4) * [1312, 1696, 5569, 124, 8283, 5886;
               2329, 4135, 8307, 3736, 1004, 9991;
               2348, 1451, 3522, 2883, 3047, 6650;
               4047, 8828, 8732, 5743, 1091, 381];
 
outer = 0;
for ii = 1:4
        inner = 0;
        for jj = 1:6
               xj = xx(jj);
               Aij = A(ii, jj);
               Pij = P(ii, jj);
               inner = inner + Aij*(xj-Pij)^2;
        end
        new = alpha(ii) * exp(-inner);
        outer = outer + new;
end
 
y = -outer;
 
end
 تابع Langermann
تابع آن به صورت زیر می باشد
ویژگی ها
  ابعاد :d
  عملکرد آن چندحالته می باشد و دارای تعداد زیادی مینیمم های محلی می باشدکه به صورت ناموزون توزیع شده اند. و مقادیر m، c و A توسط Molga
& Smutnicki (2005)  برای d= 2 به صورت زیر توصیه شده اند


m= 5
c= (1, 2, 5, 2, 3)
دامنه ورودی
کد متلب آن به صورت زیر می باشد
function [y] = langer(xx, m, c, A)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% LANGERMANN FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% 
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUTS:
%
% xx = [x1, x2, ..., xd]
% m  = constant (optional), with default value 5
% c  = m-dimensional vector (optional), with default value [1, 2, 5, 2, 3]
%      (when m=5)
% A  = (mxd)-dimensional matrix (optional), with default value
%      [3, 5; 5, 2; 2, 1; 1, 4; 7, 9] (when m=5 and d=2)
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
d = length(xx);
 
if (nargin < 2)
    m = 5;
end
 
if (nargin < 3)
    if (m == 5)
        c = [1, 2, 5, 2, 3];
    else
        error('Value of the m-dimensional vector c is required.')
    end
end
 
if (nargin < 4)
    if (m==5 && d==2)
        A = [3, 5; 5, 2; 2, 1; 1, 4; 7, 9];
    else
        error('Value of the (mxd)-dimensional matrix A is required.')
    end
end
 
outer = 0;
for ii = 1:m
    inner = 0;
    for jj = 1:d
        xj = xx(jj);
        Aij = A(ii,jj);
        inner = inner + (xj-Aij)^2;
    end
    new = c(ii) * exp(-inner/pi) * cos(pi*inner);
    outer = outer + new;
end
 
y = outer;
 
end
تابع Circle
تابع به صورت زیر می باشد
دامنه ورودی 
   ورودی ها در بازه [-15, 15]  می باشند
مینیمم سراسری
تابع Schwefel
تابع به صورت زیر می باشد
ویژگی های آن 
      این تابع پیوسته می باشد
    این تابع به صورت محدب نمی باشد. 
      این تابع در فضای nبعدی تعریف شده است. 
      این تابع چندحالته می باشد
دامنه ورودی
  دامنه ورودی آن هر مقداری می تواند باشد ولی معمولا به صورت زیر تعریف می شود
مینیمم سراسری
کد متلب آن به صورت زیر می باشد


% Computes the value of the Schwefel benchmark function.
% SCORES = SCHWEFELFCN(X) computes the value of the Schwefel function at 
% point X. SCHWEFELFCN accepts a matrix of size M-by-2 and returns a  
% vetor SCORES of size M-by-1 in which each row contains the function value 
% for the corresponding row of X.
% For more information please visit: 
% 
% Author: Mazhar Ansari Ardeh
function scores = schwefelfcn(x)
    n = size(x, 2);
    scores = 418.9829 * n - (sum(x .* sin(sqrt(abs(x))), 2));
end
تابع Rastrigin
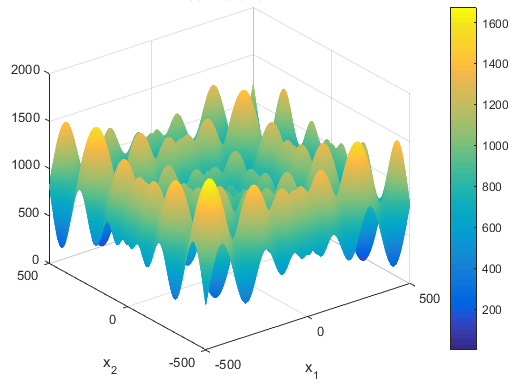
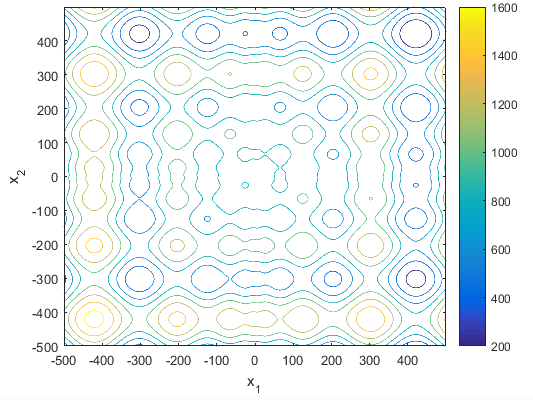
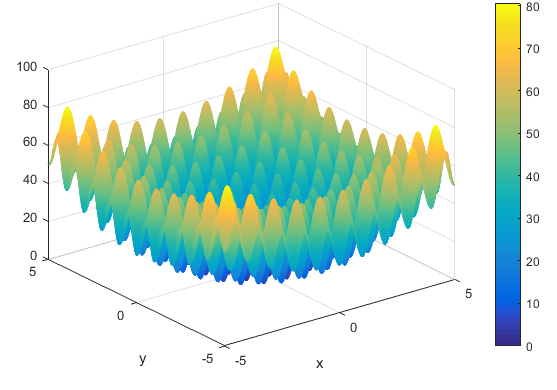
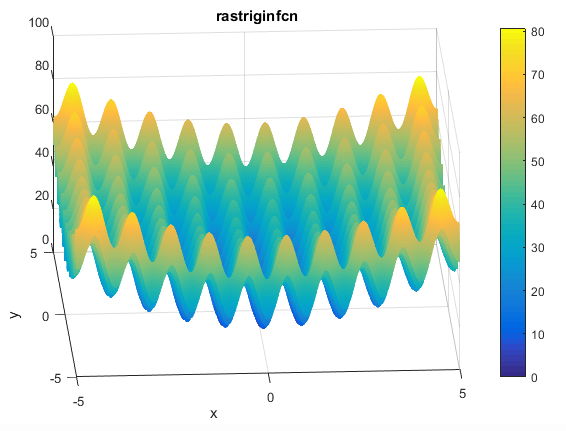
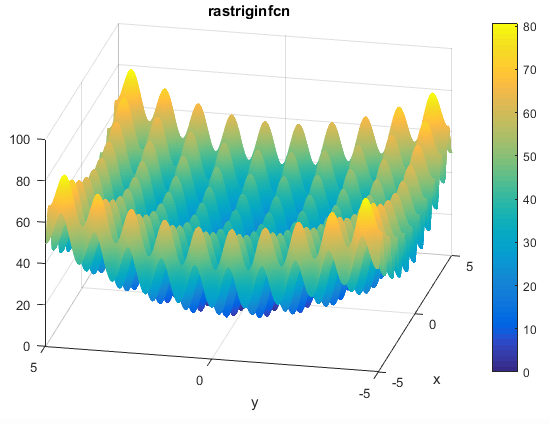
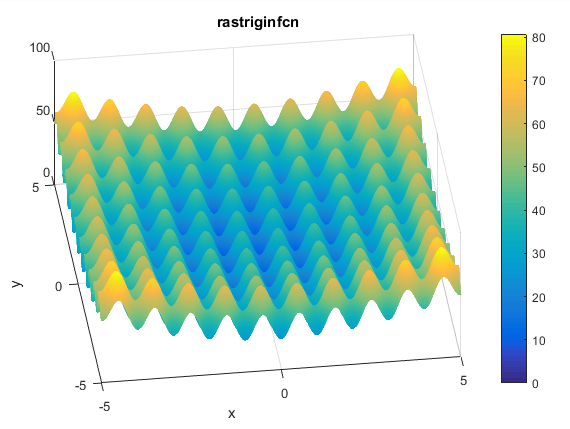
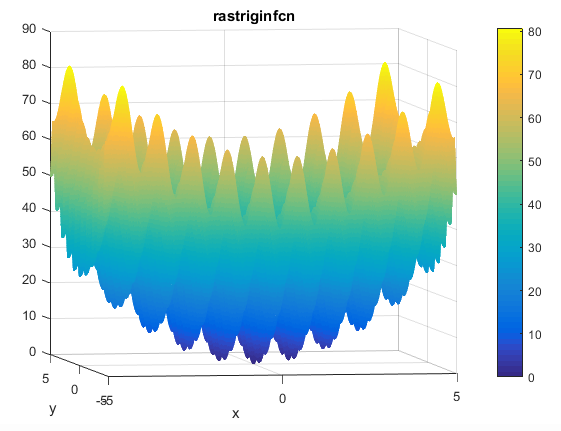
تابع آن به صورت زیر می باشد
ویژگی های آن 
     این تابع پیوسته می باشد
     این تابع به صورت محدب می باشد. 
     این تابع در فضای nبعدی تعریف شده است. 
     این تابع چندحالته می باشد
   این تابع قابل تشخیص (differentiable) می باشد
   این تابع قابل تفکیک می باشد
دامنه ورودی
  هر مقداری می تواند به عنوان ورودی در نظر گرفته شود ولی معمولا بازه زیر در نظرگرفته می شود
مینیمم سراسری
کد متلب آن به صورت زیر می باشد
% Computes the value of Rastrigin benchmark function.
% SCORES = RASTRIGINFCN(X) computes the value of the Rastrigin function at 
% point X. RASTRIGINFCN accepts a matrix of size M-by-N and returns a vetor 
% SCORES of size M-by-1 in which each row contains the function value for
% the corresponding row of X.
% For more information please visit: 
% https://en.wikipedia.org/wiki/Rastrigin_function
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function f = rastriginfcn(x)
    n = size(x, 2);
    A = 10;
    f = (A * n) + (sum(x .^2 - A * cos(2 * pi * x), 2));
end
تابع Drop-Wave
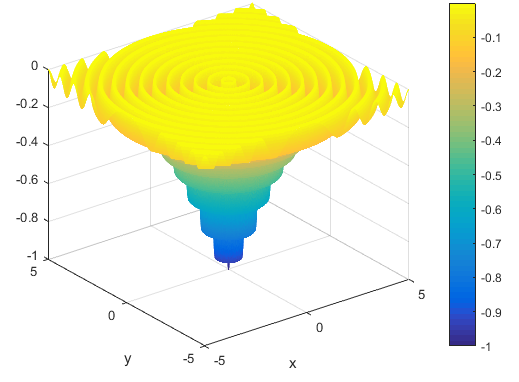
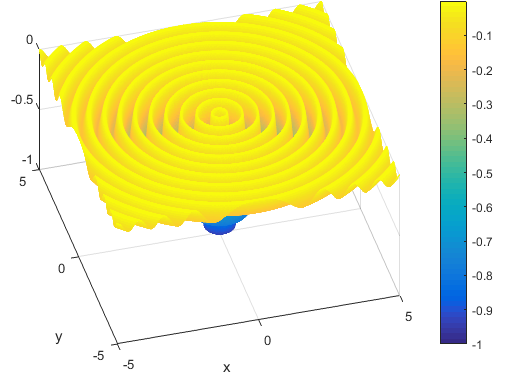
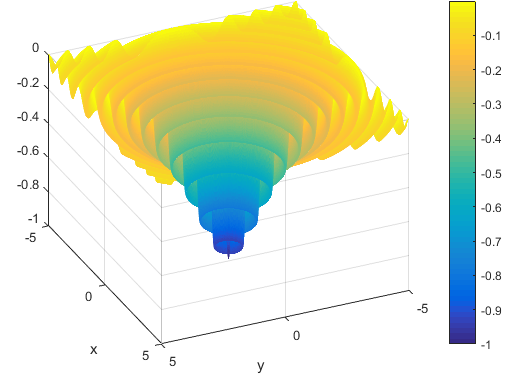
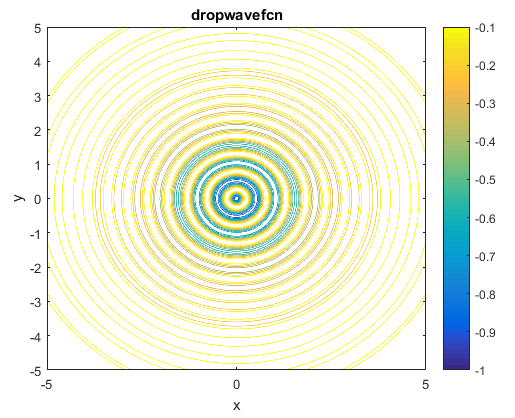
          تابع به صورت زیر می باشد 

ویژگی ها
                                         این تابع پیوسته می باشد
                                         این تابع به صورت محدب نمی باشد. 
              این تابع در فضای 2بعدی تعریف شده است. 
                                         این تابع چندحالته می باشد
دامنه ورودی
   روی هر بازه می توان آن را تعریف کرد ولی معمولا روی بازه زیر تعریف می شود
      مینیمم سراسری
      کد متلب آن به صورت زیر می باشد
% Computes the value of the Drop-Wave benchmark function.
% SCORES = DROPWAVEFCN(X) computes the value of the Drop-Wave function at 
% point X. DROPWAVEFCN accepts a matrix of size M-by-2 and returns a  
% vetor SCORES of size M-by-1 in which each row contains the function value 
% for the corresponding row of X.
% For more information please visit: 
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = dropwavefcn(x)
    n = size(x, 2);
    assert(n == 2, 'Drop-Wave function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    numeratorcomp = 1 + cos(12 * sqrt(X .^ 2 + Y .^ 2));
    denumeratorcom = (0.5 * (X .^ 2 + Y .^ 2)) + 2;
    scores = - numeratorcomp ./ denumeratorcom;
end
تابع Levi No.13
تابع به صورت زیر می باشد
دامنه ورودی
[-10,10]
مینیمم سراسری
تابع Schaffer No.2
تابع آن به صورت زیر می باشد
ویژگی ها:
این تابع پیوسته می باشد
این تابع به صورت محدب نمی باشد. 
این تابع در فضای 2بعدی تعریف شده است. 
این تابع غیربدیل(unimodal) می باشد
این تابع تشخیص پذیر(differentiable) است
این تابه تفکیک ناپذیر(non-separable) می باشد
دامنه ورودی 
روی هر بازه می توان آن را تعریف کرد ولی معمولا روی بازه زیر تعریف می شود
          مینیمم سراسری
             کد متلب آن به صورت زیر می باشد
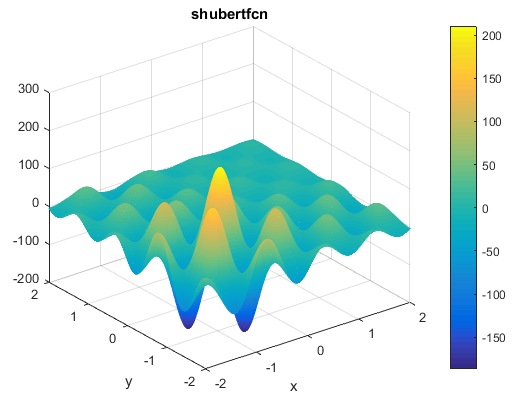
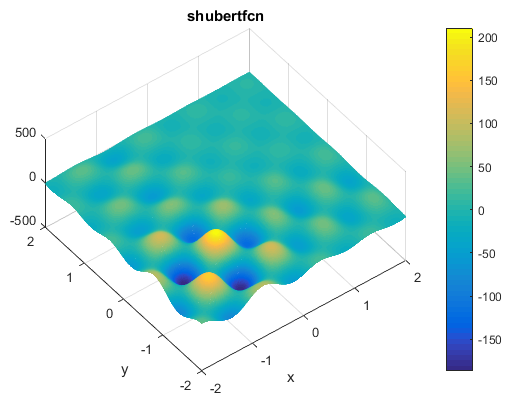
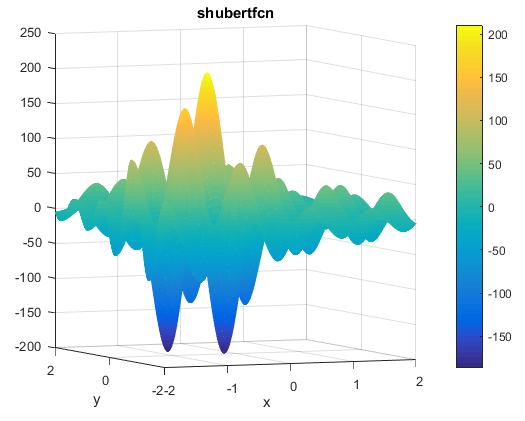
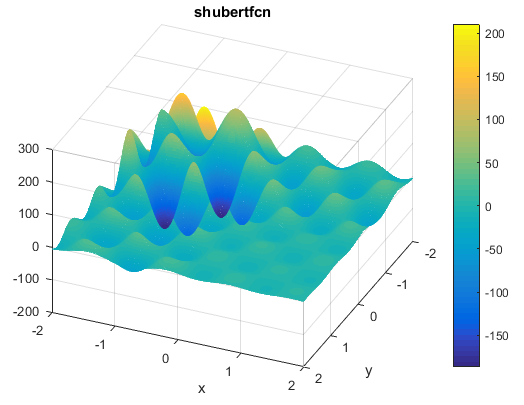
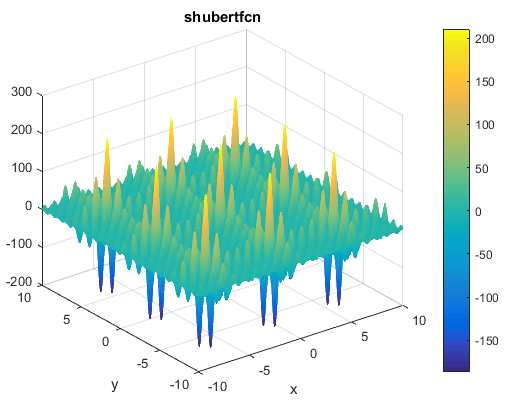
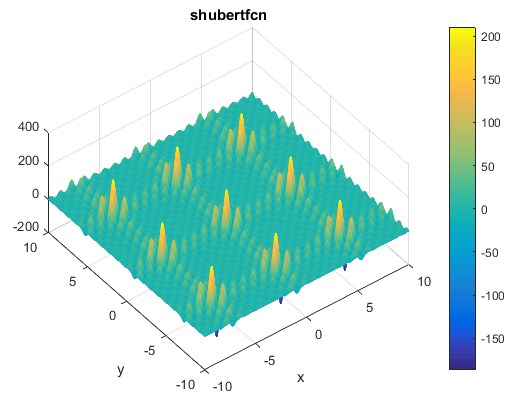
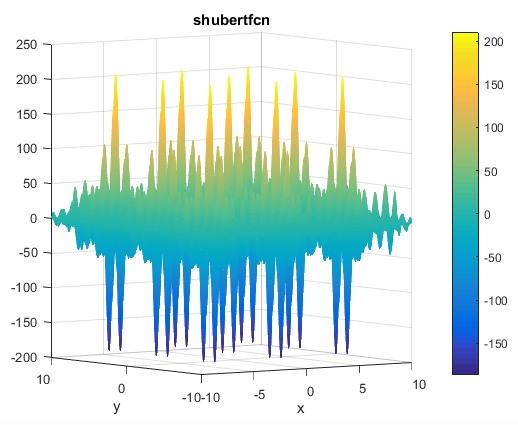
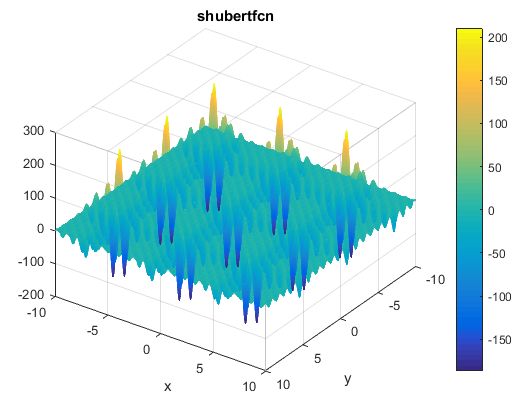
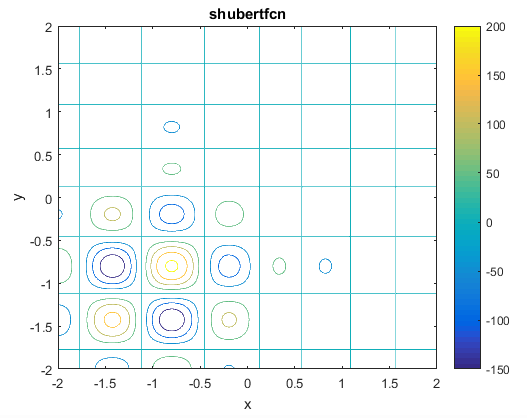
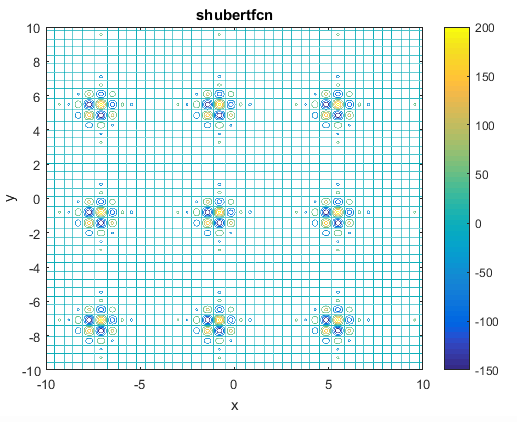
% Computes the value of the Schaffer N. 2 benchmark function.
% SCORES = SCHAFFERN2FCN(X) computes the value of the Schaffer N. 2 function 
% at point X. SCHAFFERN2FCN accepts a matrix of size M-by-2 and returns a 
% vetor SCORES of size M-by-1 in which each row contains the function value 
% for the corresponding row of X. For more information please visit: 
% https://en.wikipedia.org/wiki/Test_functions_for_optimization
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = schaffern2fcn(x)
    
    n = size(x, 2);
    assert(n == 2, 'The Schaffer N. 2 function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    sincomponent = sin( (X .^ 2) - (Y .^ 2) ).^2;
    
    scores = 0.5 + ((sincomponent - 0.5) ./ (1 + 0.001 * (X .^2 + Y .^2)) .^2 ) ;
end
تابع Shubert
تابع به صورت زیر تعریف می شود
ویژگی ها:
                             این تابع پیوسته می باشد
   این تابع به صورت محدب نمی باشد. 
   این تابع در فضای nبعدی تعریف شده است. 
   این تابع چندحالته می باشد
 این تابع تشخیص پذیر(differentiable) است
 این تابه تفکیک ناپذیر(non-separable) می باشد
دامنه ورودی
   روی هر بازه می توان آن را تعریف کرد ولی معمولا روی بازه زیر تعریف می شود
                مینیمم سراسری
                        این تابع 18 تا مینیمم سراسری دارد 
                   کد متلب آن به صورت زیر می باشد
% Computes the value of the Shubert function.
% SCORES = SHUBEERTFCN(X) computes the value of the Shubert 
% function at point X. SHUBEERTFCN accepts a matrix of size M-by-N and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X.
% See also: shubert3fcn, shubert4fcn
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = shubertfcn(x)
    n = size(x, 2);
    
    scores = 1;
    for i = 1:n
        inner_sum = 0;
        for j = 1:5
            inner_sum = inner_sum + j * cos(((j + 1) * x(:, i)) + j);
        end
        scores = inner_sum .* scores;
    end
end
تابع Price No.2
تابع آن به صورت زیر می باشد
دامنه ورودی :
[-10, 10]
مینیمم سراسری
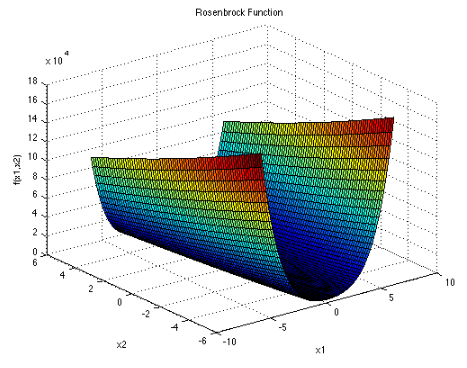
تابع Rosenbrook
ویژگیها 
    این تابع در فضای d بعدی تعریف شده است. 
دامنه ورودی
مینیمم سراسری
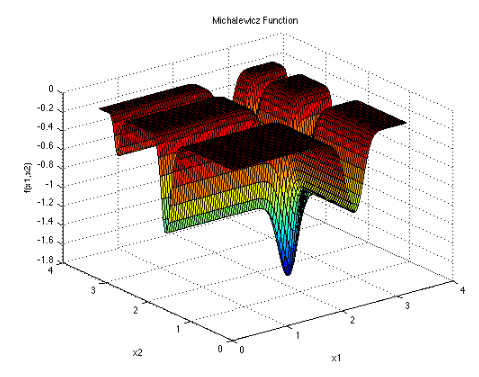
تابع Michalewicz
تابع آن به صورت زیر است
ویژگی ها
    این تابع در فضای d بعدی تعریف شده است. 
دامنه ورودی
مینیمم سراسری
کد متلب آن به صورت زیر است
function [y] = michal(xx, m)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% MICHALEWICZ FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUTS:
%
% xx = [x1, x2]
% m = constant (optional), with default value 10
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
if (nargin == 1)
    m = 10;
end
 
d = length(xx);
sum = 0;
 
for ii = 1:d
        xi = xx(ii);
        new = sin(xi) * (sin(ii*xi^2/pi))^(2*m);
        sum  = sum + new;
end
 
y = -sum;
 
end
 تابع Six-Hump Camel
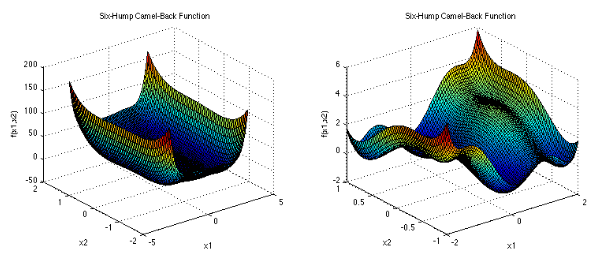
تابع آن به صورت زیر می باشد
ویژگیها
                                            این تابع در فضای 2بعدی تعریف شده است.
                                            دارای 6 تا مینیمم محلی و دو تا مینیمم سراسری می باشد
    دامنه ورودی
    مینیمم سراسری
                 کد متلب آن به صورت زیر می باشد
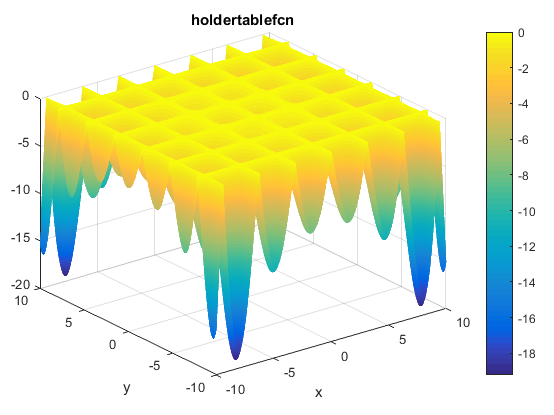
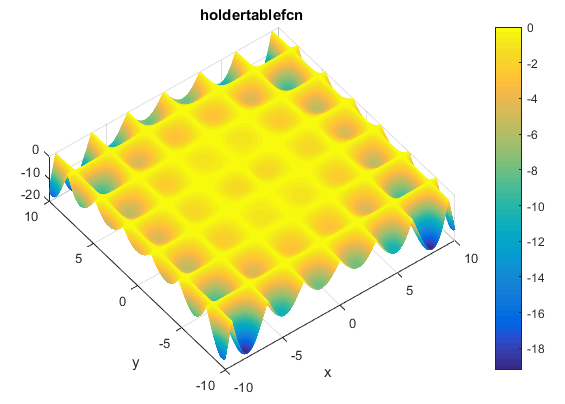
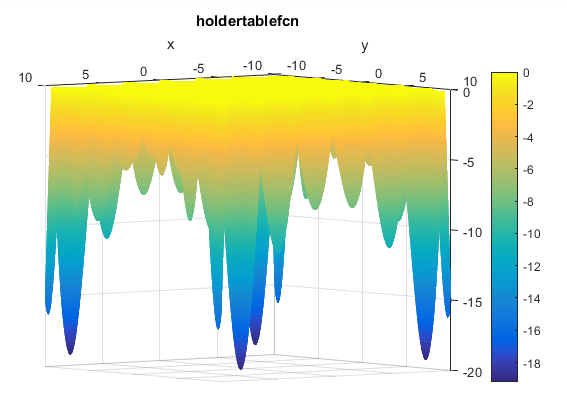
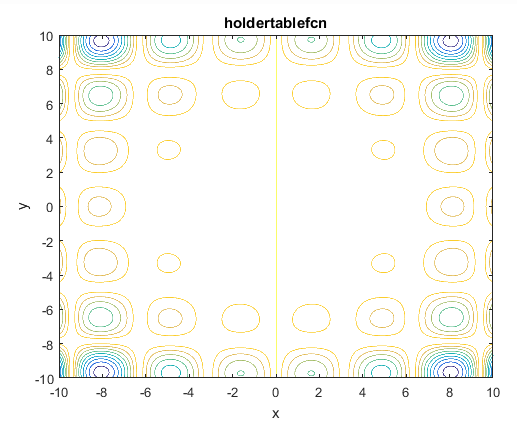
function [y] = camel6(xx)
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% SIX-HUMP CAMEL FUNCTION
%
% Authors: Sonja Surjanovic, Simon Fraser University
%          Derek Bingham, Simon Fraser University
% Questions/Comments: Please email Derek Bingham at dbingham@stat.sfu.ca.
%
% Copyright 2013. Derek Bingham, Simon Fraser University.
%
% THERE IS NO WARRANTY, EXPRESS OR IMPLIED. WE DO NOT ASSUME ANY LIABILITY
% FOR THE USE OF THIS SOFTWARE.  If software is modified to produce
% derivative works, such modified software should be clearly marked.
% Additionally, this program is free software; you can redistribute it 
% and/or modify it under the terms of the GNU General Public License as 
% published by the Free Software Foundation; version 2.0 of the License. 
% Accordingly, this program is distributed in the hope that it will be 
% useful, but WITHOUT ANY WARRANTY; without even the implied warranty 
% of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 
% General Public License for more details.
%
% For function details and reference information, see:
% http://www.sfu.ca/~ssurjano/
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% INPUTS:
%
% xx = [x1, x2]
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
x1 = xx(1);
x2 = xx(2);
 
term1 = (4-2.1*x1^2+(x1^4)/3) * x1^2;
term2 = x1*x2;
term3 = (-4+4*x2^2) * x2^2;
 
y = term1 + term2 + term3;
 
end
تابع Holder
تابع آن به صورت زیر تعریف می شود
ویژگی ها:
این تابع پیوسته می باشد
این تابع به صورت محدب نمی باشد. 
این تابع در فضای nبعدی تعریف شده است. 
این تابع چندحالته می باشد
این تابع تشخیص پذیر(differentiable) است
این تابه تفکیک ناپذیر(non-separable) می باشد
دامنه ورودی
روی هر بازه می توان آن را تعریف کرد ولی معمولا روی بازه  زیر تعریف می شود
                مینیمم سراسری
                  کد متلب آن به صورت زیر می باشد
% Computes the value of the Holder table benchmark function.
% SCORES = HOLDERTABLEFCN(X) computes the value of the Holder table  
% function at point X. HOLDERTABLEFCN accepts a matrix of size M-by-2 and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X. For more information 
% please visit: 
% https://en.wikipedia.org/wiki/Test_functions_for_optimization
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = holdertablefcn(x)
    
    n = size(x, 2);
    assert(n == 2, 'The Holder-table function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    expcomponent = exp( abs(1 - (sqrt(X .^2 + Y .^ 2) / pi)) );
    
    scores = -abs(sin(X) .* cos(Y) .* expcomponent);
end
تابع Trigonometric
تابع به صورت زیر می باشد
دامنه ورودی
                  [-500, 500]
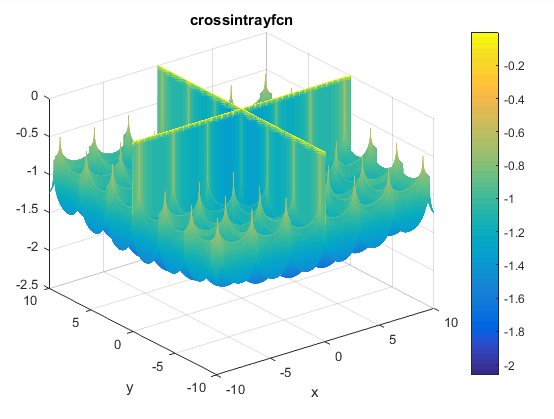
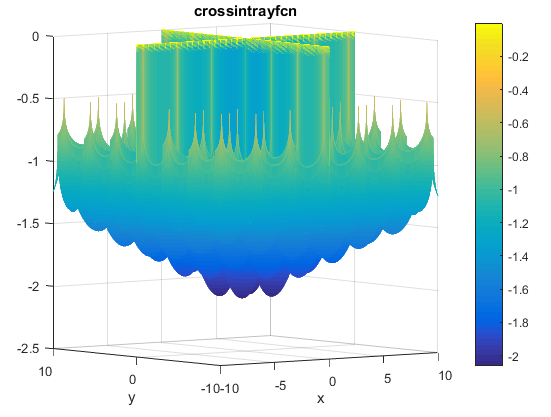
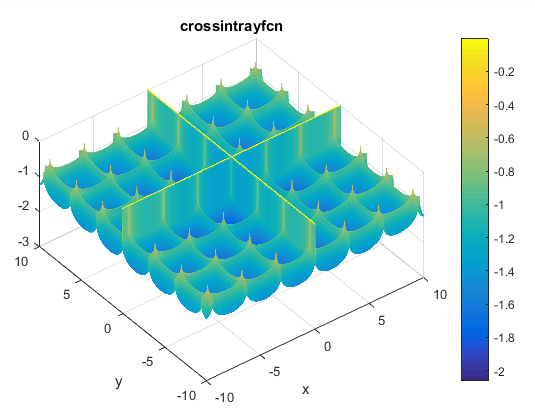
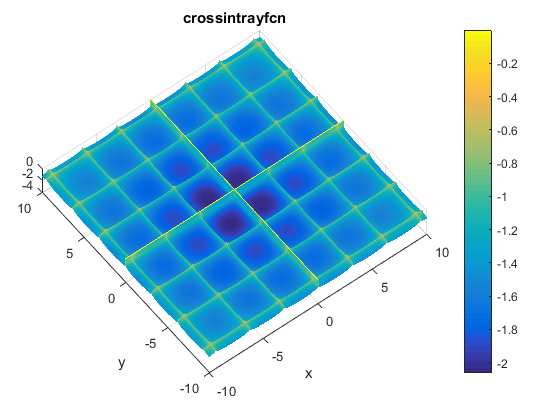
                 مینیمم سراسری
تابع Cross-in-Tray
تابع آن به صورت زیر می باشد


ویژگی ها:
این تابع پیوسته می باشد
این تابع به صورت محدب نمی باشد. 
این تابع در فضای 2بعدی تعریف شده است. 
این تابع چندحالته(multimodal) می باشد
این تابع تشخیص پذیر(differentiable) است
  دامنه ورودی
       روی هر بازه می توان آن را تعریف کرد ولی معمولا روی بازه  زیر تعریف می شود
مینیمم سراسری
کد متلب آن به صورت زیر می باشد
% Computes the value of the Cross-in-tray benchmark function.
% SCORES = CROSSINTRAYFCN(X) computes the value of the Cross-in-tray 
% function at point X. CROSSINTRAYFCN accepts a matrix of size M-by-2 
% and returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X. For more information 
% please visit: 
% https://en.wikipedia.org/wiki/Test_functions_for_optimization
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = crossintrayfcn(x)
    
    n = size(x, 2);
    assert(n == 2, 'The Cross-in-tray function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
 
    expcomponent = abs(100 - (sqrt(X .^2 + Y .^2) / pi));
    
    scores = -0.0001 * ((abs(sin(X) .* sin(Y) .* exp(expcomponent)) + 1) .^ 0.1);
end


Mojgan Abtahi یکشنبه 19 مرداد 1399 ساعت 02:45
نظرات 0 + ارسال نظر
برای نمایش آواتار خود در این وبلاگ در سایت Gravatar.com ثبت نام کنید. (راهنما)
ایمیل شما بعد از ثبت نمایش داده نخواهد شد